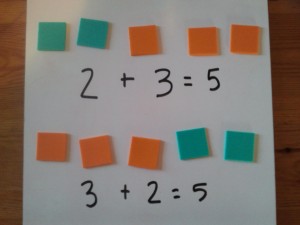Making sense of and understanding mathematics is the foundation of the new Common Core State Standards in Mathematics.  It is not enough that kids can compute with numbers – they must understand why those computations work.  Enter Number Theory, the part of math that explores numbers and how they relate to each other. 

At the heart of Number Theory are the properties of number.  One of the first ones students will encounter is the Commutative Property of Addition.  It states that a + b = b + a.  In other words, 2 + 3 = 3 + 2.  And since the Standards emphasize the equal sign to mean is the same as, then students will soon become comfortable with the Commutative Property.  (BTW, we don’t need to use the words ‘commutative property’ in the primary grades; the concept is what’s important.)

The photo illustrates a simple way to get students to physically see the commutative property in action.  I was doing a similar activity in kindergarten a number of years ago and one of the students blurted out, “Hey, it’s the same.  They’re just opposite!”  It’s fun to see that lightbulb go on.

So why is it important to focus on the commutative property?  For one, it represents turnaround facts: 4 + 6 = 6 + 4 means we only have to learn one, 4 + 6, to know the other, 6 + 4.  This becomes increasingly important as students begin to study multiplication and can tap into the Commutative Property of Multiplication to learn all their facts:  4 x 6 = 6 x 4.

But understanding the properties (I’ll be sharing more in upcoming blogs) also shows how numbers relate to each other and how they can be “manipulated” to make working with them easier.  In other words, numbers should make sense.  And they make sense in different ways depending on the student.  The beauty of that is that we will all arrive at the same place, we just may take a different route.  And there’s nothing wrong with that.

So as your students/children are learning their number facts, ask them questions like, “Hey, is 5 + 4 the same as 4 + 5? How do you know?” Providing them with concrete objects to use as counters can help them verbalize and solidify what they’re sorting through in their heads.